Ordet procent kommer från latin och betyder “för hundra” eller “av hundra”. Det används till att ange en proportion av någonting, där 100 motsvarar hela och 0 inget.
Procent brukar betecknas med tecknet %. Det finns flera sätt att räkna procent. Hur man gör beror på vilket svar man vill komma fram till och vilka förhandsuppgifter man har. Den här artikeln handlar om olika sätt att räkna procent. Artikeln berättar både om vilka situationer procenträkning behövs i och hur man ska gå tillväga för att få ett svar. Räkneinstruktionerna ges numrerade steg för steg för att det ska bli lätt att följa dem.
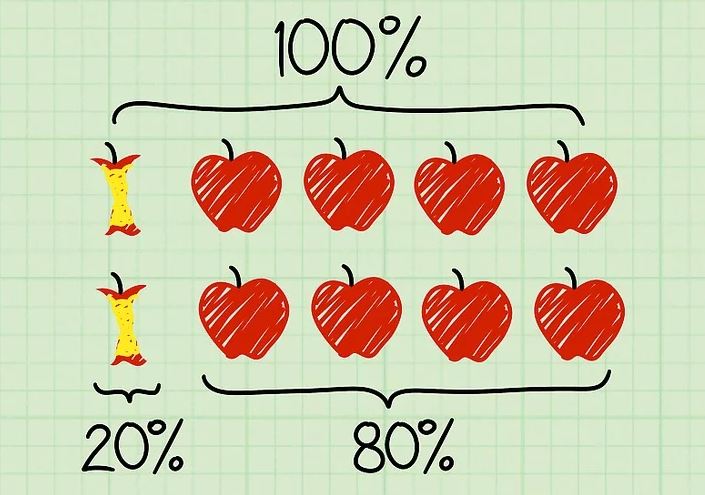
Räkna äpplen
Procenträkning kan användas till flera olika typer av räkneuppgifter. Procent gör det lättare att ange en proportion av något, då man kan ange andelen istället för antalet. Ett exempel är att man istället för att säga “Solen sken 30 dagar av 100” kan säga “Solen sken 30 % av tiden”, vilket är ett tydligare och mer generellt sätt att säga samma sak. Man har alltså angett andelen tid då solen sken istället för att rakt av ange tiden. I den här artikeln visas hur detta ska räknas tillsammans med några andra sätt att räkna procent, med både allmän information om när räknesättet används och instruktioner gällande räkneprocessen.
Räkna ut procent av en helhet
Det vanligaste är måhända att räkna ut en andel av en helhet i procent. Då vill man utreda hur många procent en mindre del utgör av helheten. Vi kan använda vårt tidigare exempel om 30 soliga dagar av 100. Vi kom fram till att de 30 soliga dagarna motsvarade 30 % av helheten, vilken i detta fall var 100 dagar, men hur ska man tänka för att komma fram till det svaret? Instruktionerna till denna räkneuppgift består av några ganska enkla steg, vilka går att applicera på uppgifter där syftet är att utreda en mindre dels proportion av den större helheten.
Vi vill utreda hur många procent 30 dagar är av 100. 100 är i detta fall vår helhet och 30 är den mindre delen vars andel vi vill undersöka. Gör såhär: 1. Skriv ut värdena i bråkform så att du har delen du vill undersöka först och sedan helheten: 30/100. 2. Dividera 30 med 100 för att omvandla värdet till decimalform: 30/100=0,3. 3. Konvertera decimalen till procent genom att multiplicera med 100: 0,3×100=30. Svaret du får i steg tre motsvarar den procentuella andelen av delen vi ville undersöka, alltså är svaret att de soliga dagarna utgör 30 % av tiden.

Procentberäkning kan hjälpa dig i finansiering
Räkna ut en siffra utgående från procent
I vissa fall kanske vi redan vet procentandelen av något och då vill vi kanske veta vilken siffra som motsvaras av procentandelen. Ett typiskt exempel här är när vi vill räkna ut storleken på en låneränta. Då vet vi hur mycket vi har lånat och vi vet också räntan angiven i procent. Då kanske vi vill räkna ut hur stor räntan är per dag i pengar. Vi kan säga att vi har lånat 150 kronor av en kompis och kompisen kräver 3 % i ränta per dag. Dessa är de siffror vi behöver känna till för att räkna ut storleken på den dagliga räntan.
Gör enligt stegen nedan: 1. Dividera procentandelen med 100 för att få den omvandlad till decimalform: 3/100=0,03. 2. Multiplicera den lånade summan med decimalen: 150×0,03=4,50. Svaret du får i steg två motsvarar den dagliga räntan, alltså är räntan 4,50 kronor per dag. Om du behöver utreda summan med ränta inkluderad för flera dagar adderar du den ursprungliga lånade summan med räntan gånger antalet dagar, enligt följande: 150+(4,50 x antalet dagar). Om du exempelvis vill utreda vad hela summan blir för fem dagar använder du formeln 150+(4,50×5)=172,50. Därmed kan vi fastslå att hela summan inklusive ränta för fem dagar blir 172,50 kronor.
Procenträkning av rabatterade priser
Rabatter i butiker brukar anges i procent. Vissa butiker gör en rabattabell till kunderna för att kunden inte ska behöva räkna de rabatterade priserna själva men det går även snabbt och enkelt att räkna ut de rabatterade priserna själv. Vi kan säga att vi har en produkt som tidigare har kostat 200 kronor och nu säljs för 30 % rabatterat pris. Här kan man göra på två olika sätt – antingen räkna bort den summa man inte ska betala, i det här fallet 30 %, eller så kan man välja att räkna ut det pris som man ska betala, alltså 70 %. Vi kommer räkna ut 70 % i exemplet nedan.

Procentberäkning kan vara svårt
Vi kommer räkna ut både den nya köpesumman och den summa pengar vi sparar in på köpet av den rabatterade produkten. Gör såhär: 1. Dividera 70 med 100 för att få en decimal: 70/100=0,7. 2. Multiplicera det ursprungliga priset med decimalen: 200×0,7=140 3. Subtrahera det ursprungliga priset med det nya priset: 200-140=60. Svaret i steg två är det nya priset och svaret i steg tre är den summa pengar som sparas in på köpet då produkten är rabatterad. Således betalar vi 140 kronor för produkten och vi sparar in 60 kronor på köpet när produkten säljs till 30 % rabatterat pris.
Statistik
I räkneexemplen ovan har vi alltid omvandlat procenten till en decimal för att lättare kunna göra de uträkningar som krävs. Procenten är i grunden ett sätt att formatera det matematiska svaret. I statistik är det vanligt att man använder decimaler istället för att skriva ut procent. Liksom vi gjorde i exemplen används då siffrorna 0-1 för att motsvara procentandelen av en helhet. Inom statistik anges ofta proportioner med en siffra inom intervallet 0-1 men det går lätt att formatera om svaret till procentform genom att multiplicera decimalen med 100. Således får vi exempelvis 78 % till svar, om ett statistiskt resultat visar 0,78, detta eftersom 0,78×100=78.
Sammanfattning
Som vi har kunnat se finns procenträkningen med i flera olika matematiska problem. I korthet kan vi säga att procenträkning används när vi vill uttrycka en förändring eller en proportion av något, vilket vi har kunnat se i denna artikel. Vi har utrett procentandel av en helhet när vi räknade ut antalet soliga dagar, vi har räknat ut vilken summa en räntesats motsvarar när vi räknade med pengarna som lånats av en kompis, vi har räknat ut rabatterade priser och slutligen diskuterat kort hur statistiken behandlar procentandelar. Andra proportionsuttryck inkluderar promille, vilket anger tusendelar och vanligen används till att räkna ut alkoholhalt.